Физика 2
Билет 10.
10.1. Второй закон Ньютона
Произведение массы тела на вектор ускорения тела равно вектору равнодействующей сил, действующих на тело.
Вектор силы сонаправлен с вектором ускорения, так как масса - это положительная величина.
Второй закон Ньютона работает только в инерциальных системах отсчёта.
10.2. Вывод закона движения материальной точки под действием постоянной силы
Мы можем получить закон движения материальной точки для равномерного и равнопеременного движения, проинтегрировав второй закон Ньютона.
10.3. Третий закон Ньютона
Два тела действуют друг на друга с силами, равными по модулю, противоположными по направлению.
Эти силы имеют одну и ту же физическую природу и направлены вдоль одной прямой, соединяющей их точки приложения.

10.4. Неинерциальные системы отсчёта
Система отсчёта, связанная с телом, движущимся относительно инерциальной системы отсчёта, с некоторым ускорением, называется неинерциальной системой отсчёта.

10.5. Поступательные и центробежные силы инерции
В неинерциальной системе отсчёта существуют силы, которые не существуют в инерциальной системе отсчёта.
Они нужны для того, чтобы в неинерциальной системе отсчёта выполнялся второй закон Ньютона.
Существуют два типа сил инерции:
При поступательном движении тела относительно неинерциальной системы отсчёта существует сила инерции, направленная противоположно ускорению тела.
При вращательном движении тела относительно неинерциальной системы отсчёта существует центробежная сила инерции, направленная от центра вращения.

Билет 11.
11.1. Закон всемирного тяготения
Любые два материальных тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

11.2. Гравитационная постоянная и её измерение Кавендишем
Гравитационная постоянная - это коэффициент пропорциональности в законе всемирного тяготения.
Опыт Кавендиша
В 1798 году Кавендиш измерил гравитационную постоянную, используя крутильные весы.

Насколько я понял, подвесили два тяжелых шара на проволоку, заранее посчитали силу упругости при малых углах отклонения, потом посчитали силу притяжения между шарами, зная массы шаров и расстояние между ними.
11.3. Сила тяжести
Сила тяжести - это сила гравитационного притяжение, действующая на тело со стороны планеты (Земли).
11.4. Зависимость силы тяжести от высоты
Сила тяжести убывает в геометрической прогрессии с увеличением высоты.
11.5. Вес тела, невесомость и перегрузки
Вес тела - это сила, с которой тело действует на опору.
Невесомость - это когда вес тела меньше силы тяжести.
Перегрузка - это когда вес тела больше силы тяжести.
11.6. Вес тела, находящегося на поверхности Земли, и его зависимость от географической широты.
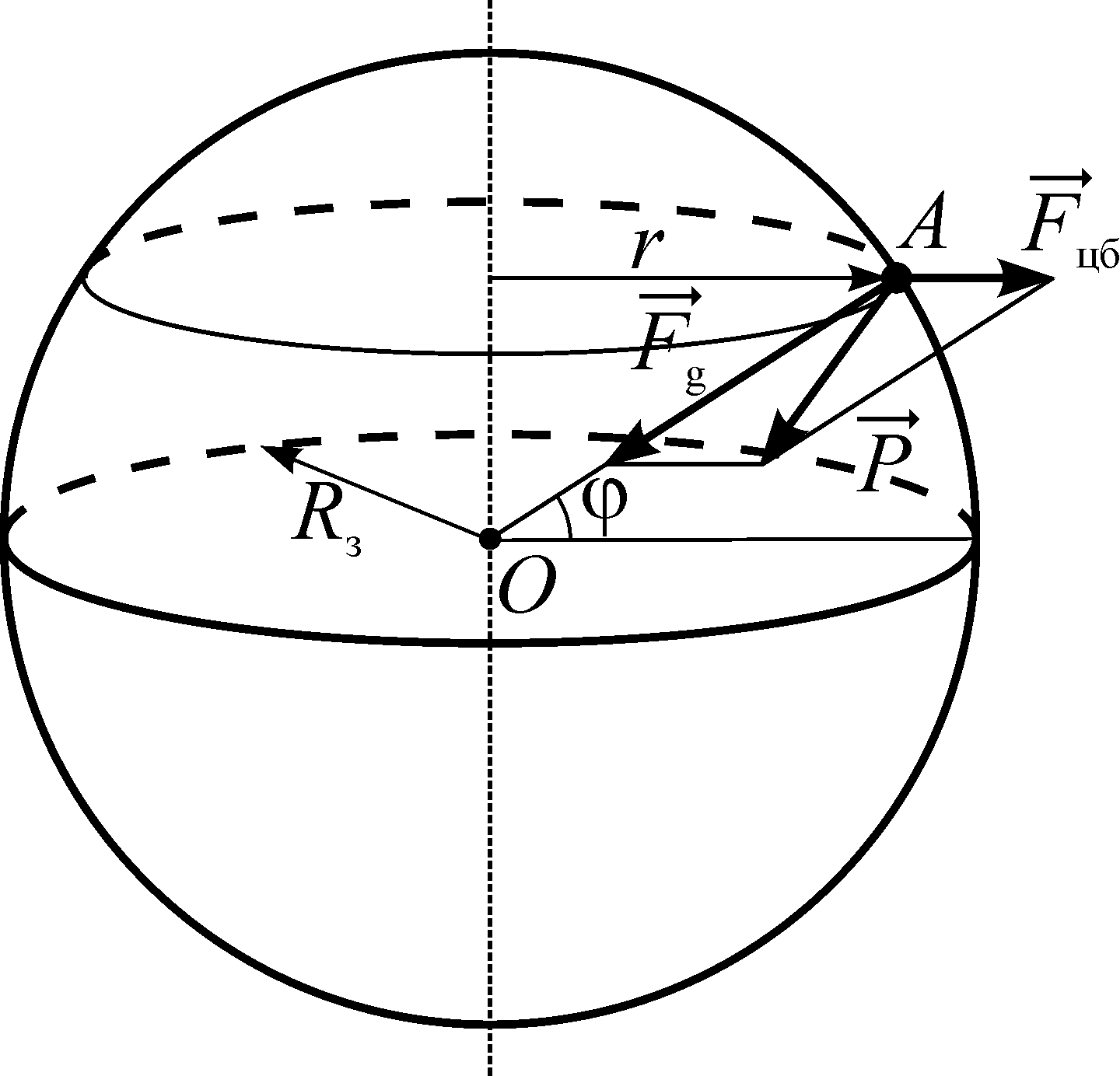
Билет 12.
12.1. Движение искусственных спутников Земли

Из рисунка видно, что радиус есть сумма радиуса Земли и высоты спутника.
12.2. Первая космическая скорость
Первая космиеская скорость - это минимальная скорость, с которой нужно запустить тело, чтобы оно не падало на Землю.
Это минимальная скорость, так как высота спутника не может быть меньше нуля, а скорость прямо пропорциональна квадратному корню из суммы радиуса Земли и высоты спутника.
12.3. Законы Кеплера
12.3.1. Первый закон Кеплера
Первый закон Кеплера - все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.
Так происходит потому, что Солнце имеет невероятно большую массу, не сравнимую с массой планет, поэтому можно считать, что Солнце неподвижно.

12.3.2. Второй закон Кеплера
Второй закон Кеплера - радиус-вектор, проведённый из Солнца к планете, за равные промежутки времени, заметает равные площади.
Доказательство не требуется, т.к. это дичь!

12.3.3. Третий закон Кеплера
Третий закон Кеплера - квадраты периодов обращения планет пропорциональны кубам больших полуосей их орбит.

Вывод
Билет 13.
13.1. Силы упругости
Силы упругости - это силы, возникающие в теле при сжатии или растяжении тела.
Причём силы упругости направлены так, чтобы вернуть тело в исходное состояние и возникают только у упругих тел.

13.2. Упругие и пластические деформации
Упругие деформации - это деформации, которые исчезают после прекращения действия силы.
Пластические деформации - это деформации, которые не исчезают после прекращения действия силы.

13.3. Закон Гука
Закон Гука - деформация тела прямо пропорциональна силе, вызвавшей эту деформацию.

13.4. Модуль Юнга и его взаимосвязь с коэффициентом упругости
Модуль Юнга - это модуль упругости первого рода, который характеризует упругие свойства тела при одноосном растяжении.
13.5. Физический смысл модуля Юнга
Модуль Юнга показывает, с какой силой надо сжать или растянуть стержень единичного поперечного сечения, чтобы получилось изменение длины на единицу.
Билет 14.
14.1. Силы трения
Силы трения - это силы, возникающая при соприкосновении двух тел и препятствующая их относительному движению.

Она направлена противоположно относительному движению тел.
14.2. Виды сил трения
Существует два вида сил сухого трения:
Сила трения покоя - сила трения, возникающая при отсутствии относительного движения тел.
Сила трения скольжения - сила трения, возникающая при относительном движении тела и опоры.
14.3. Коэффициент трения
Коэффициент трения - это безразмерная величина, характеризующая силу трения.
14.4. Направление сил сухого трения
Силы сухого трения направлены противоположно относительному движению тел.

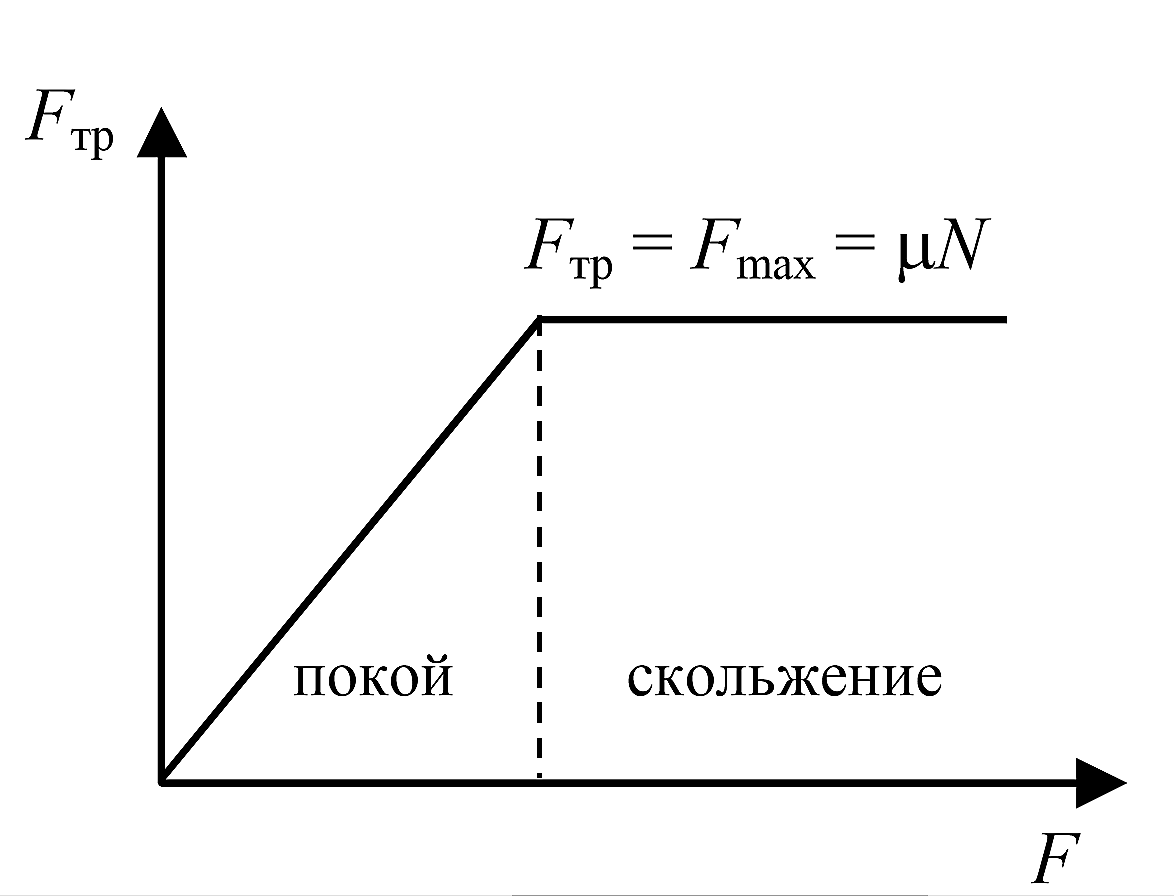
14.5. Зависимость силы сухого трения от внешней силы
В случае силы трения покоя сила трения не может превышать силу, приложенную к телу.
По этой причине, сила трения покоя возрастает с увеличением внешней силы, пока не достигнет максимального значения.
В случае если оно превышает максимальное значение, тело начинает двигаться, а сила трения становится равной силе трения скольжения.
Для лучшего понимания, посмотрите на график зависимости силы трения от внешней силы.
14.6. Вязкое трение
Вязкое трение - это сила трения, возникающая при движении тела в жидкости или газе.

Зависимость силы вязкого трения от скорости
Билет 15.
15.1. Импульс материальной точки
Импульс материальной точки - это векторная величина, равная произведению массы материальной точки на её скорость.
15.2. Изменение импульса
Есть разность между импульсом в конечный момент времени и импульсом в начальный момент времени.
15.3. Второй закон Ньютона в импульсной форме
Простым дифференцированием можно прийти к следующему выражению:
15.4. Импульс силы
Импульс силы - это разность между импульсом в конечный момент времени и импульсом в начальный момент времени.
15.5. Импульс системы материальных точек
Начнём с простой системы из двух материальных точек.

Добавим внутренние силы, действующие в системе.
Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе.
Проведя аналогичные рассуждения несложно понять, что и импульс системы материальных точек будет иметь следующий вид:
15.6. Закон сохранения импульса
Закон сохранения импульса - это закон, согласно которому импульс замкнутой системы материальных точек с течением времени не меняется.
В этом легко убедиться, так как скорость изменения импульса системы материальных точек равна нулю, если в системе нет внешних сил.
Подобные рассуждения можно проводить и отдельно с осями координат.
15.7. Закон сохранения проекции импульса
Закон сохранения проекции импульса получается из закона сохранения импульса.
Для примера рассмотрим закон сохранения проекции импульса на ось Ox.
Билет 16.
16.1. Центр масс системы материальных точек
Центр масс системы материальных точек - это воображаемая точка (мы не придумываем её, она просто не закреплена каким-то конкретным телом), которая движется так, как если бы вся масса системы была сосредоточена в этой точке.

16.2. Импульс твёрдого тела
Твёрдое тело состоит из нескольких материальных точек, поэтому импульс твёрдого тела есть сумма импульсов всех материальных точек, из которых состоит тело.
Вывод
16.3. Способ вычисления координат центра масс
В векторной форме центр масс можно вычислить по следующей формуле:
Аналогично можно вывести для проекций на оси координат.
16.4. Теорема о движении центра масс
Теорема о движении центра масс - это теорема, согласно которой ускорение центра масс системы материальных точек равно векторной сумме всех внешних сил, действующих на систему.
Вывод
Как следствие из теоремы о движении центра масс, ясно, что если в системе нет внешних сил, то центр масс системы материальных точек движется равномерно и прямолинейно.
Билет 17.
17.1. Реактивное движение
Реактивное движение - это движение тела переменной массы.
Простой пример реактивного движения - это движение шарика, который теряет массу при движении.

Важно отметить, что реактивная сила возникает без какого-либо взаимодействия с внешними телами.
17.2. Уравнение Мещерского
Уравнение Мещерского - гласит о следующем:
Вывод


17.3. Реактивная сила
Реактивная сила - это сила, возникающая при реактивном движении.
Билет 18.
18.1. Механическая работа
Механическая работа - это скалярная величина, равная произведению векторов силы и перемещения тела.
Для работы есть своя единица измерения - джоуль.

18.2. Относительность работы
Относительность работы - это тот факт, что работа приложенной силы имеют одинаковую величину для всех инерциальных систем отсчёта.
18.3. Работа постоянной и переменной силы
18.4. Графический способ вычисления работы
Как пример можно привести работу силы упругости. Рассмотрим график зависимости силы упругости от перемещения тела.

18.5. Аддитивность работы
Аддитивность работы - это тот факт, что работа равнодействующей силы равна сумме работ всех сил, действующих на тело.
18.6. Мощность постоянной и переменной силы
Мощность - это физическая величина, которая показывает скорость выполнения работы и равна отношению работы к времени.
Билет 19.
19.1. Механическая энергия
Механическая энергия - это мера движения и взаимодействия механических объектов, которая равна сумме кинетической и потенциальной энергии.
19.2. Кинетическая энергия материальной точки и системы материальных точек
Кинетическая энергия материальной точки - это один из видов механической энергии, который равен половине произведения массы материальной точки
19.3. Теорема об изменении кинетической энергии
Изменение кинетической энергии равно работе, совершённой приложенными к телу внешними силами за определённый промежуток времени.
Как следствие:
Если работа внешних сил положительна, то кинетическая энергия возрастает.
Если работа внешних сил отрицательна, то кинетическая энергия убывает.
20. Продолжение...
Читайте дальше в следующей части.