Физика 1

1.0. Основная задача механики

Основная задача механики - это определение положение движущегося тела в любой момент времени.

1.1. Механическое движение

Механическое движение - это изменение положения тела в пространстве относительно других тел с течением времени.

1.2. Различные способы описания движения

Существует 3 способа описания движения:

1. Табличный

2. Графический

3. Аналитический

1.3. Системы отсчёта

Система отсчёта - это тело отсчёта вместе с которой жётско связана система координат, а так же время (начиная с некоторого момента времени).

1.4. Материальная точка

Материальная точка - это абстрактная модель, которая используется в механике, когда размеры и форма тела не играют роли, а важна только его масса и положение в пространстве.

1.5. Базовые понятия кинематики

Траектория - это линия, вдоль которой движется тело.

Путь - это длина участка траектории, пройденного телом за некоторый промежуток времени.

Перемещение - это вектор, соединяющий начальное и конечное положение тела.

Модуль перемещения (длина вектора) меньше либо равно пути.

Есть формула:

Радиус-вектор - это вектор, который соединяет начало координат и положение тела.

Есть формула модуля радиуса-вектора:

1.5.1. Виды движения

Поступательное движение - называется таковым, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно первоначальному направлению.

Вращательное движение - называется таковым, если:

1. Все точки тела описывают окружности, лежащие в параллельных плоскостях.

2. Центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям. (эта прямая называется осью вращения)

1.6. Равномерное прямолинейное движение

Равномерное прямолинейное движение - это движение по прямой, при котором тело за любые равные промежутки времени проходит одинаковые расстояния. Скорость такого движения постоянна и не зависит от времени.

1.7. Закон движения материальной точки

Закон движения материальной точки - это математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.

1.8. Графическое опиcание движения

Это способ описания движения, при котором строится график зависимости.

У графика, обычно, ось абсцисс соответствует времени, а ось ординат - координате.

2.1. Описания движения на плоскости

Движение на плоскости обычно описывается с использованием двух взаимно перпендикулярных осей “Ox” и “Oy”. В случае поступательного движения на плоскости, векторы перемещения, скорости и ускорения раскладываются на проекции по осям.

2.2. Скорость равномерного прямолинейного движения.

Определяется как отношение перемещения тела за некоторый промежуток времени к этому промежутку времени.

2.3. Средняя скорость неравномерного движения.

Определяется как отношение перемещения тела за некоторый промежуток времени к этому промежутку времени.

2.4. Мгновенная скорость.

Определяется как предел отношения перемещения тела за некоторый промежуток времени к этому промежутку времени, когда этот промежуток времени стремится к нулю.

Заметим, что мгновенная скорость - это производная радиус-вектора по времени.

3.1. Ускорение

Ускорение - это векторная величина, определяющая быстроту изменения скорости тела, её направление.

3.2. Прямолинейное движение с постоянным ускорением

Прямолинейное движение с постоянным ускорением называется равноускоренным.

Иначе говоря, если модуль скорости меняется с течением времени на постоянную величину, то такое движение называется равноускоренным.

3.3. Закон движения

Это математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют данные о движении точки.

3.4. Вывод зависимости скорости и координаты от времени

Вывод основывается на графическом представлении движения.

3.5. Графическое описание движения

Рассмотрим график зависимости координаты от времени. Это график параболы. По знаку ускорения (ускорение или торможение) можно определить направление параболы.

Теперь рассмотрим график зависимости скорости от времени. Это график прямой. По знаку ускорения (ускорение или торможение) можно определить направление прямой.

3.6. Средняя скорость равнопеременного движения

Средняя скорость равнопеременного движения - это векторная величина, по сути частный случай средней скорости неравномерного движения.

Его очень легко получить если снова обратиться к графику зависимости скоорости от времени.

4.1. Свободное падение по вертикали

Свободное падение по вертикали - это движение тела только под действием притяжения к Земле. При этом действие на тело других сил, например, силы сопротивления воздуха, не учитывается.

4.2. Движение тела, брошенного вертикально вверх

Это есть частный случай свободного падения. В этом случае начальная скорость направлена вверх, поэтому тело замедляется и в конце концов начинает падать.

4.3. Время полёта, высота подъёма.

4.4. Закон нечётных чисел для равноускоренного движения

Полное название: закон нечётных чисел для равноускоренного движения без начальной скорости.

Во сколько раз путь пройденный телом за N-ую секунду от начала равноускоренного движения больше пути, пройденного за предыдущую секунду, если движение происходит без начальной скорости?

Понять этот закон можно взглянув на следующий график зависимости скорости от времени.

5.1. Относительность движения

Относительность движения - это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Из-за этого, например, скорость тела может быть как положительной, так и отрицательной. Поэтому обязательно нужно указывать систему отсчёта, относительно которой движется тело.

Для описания полёта дрона нужно трёхмерное пространство и система отсчёта, например, связанная с Землёй.

5.2. Инерциальные системы отсчёта

Инерциальная система отсчёта - это система отсчёта, которая сохраняет свою скорость, то есть которые движутся без ускорения.

5.2.1. Силы инерции

В следствие наличия неинерциальных систем отсчёта, в механике вводятся силы инерции, которые компенсируют ускорение неподвижной системы отсчёта относительно инерциальной.

5.3. Принцип относительности Галилея

Принцип относительности Галилея - это принцип, согласно которому движущаяся система отсчёта движения без ускорения относительно неподвижной системы отсчёта является инерциальной.

Иначе говоря, на движущемся поезде (без ускорения) любое горизонтальное ускорение будет ощущаться так же, как и на неподвижной земле.

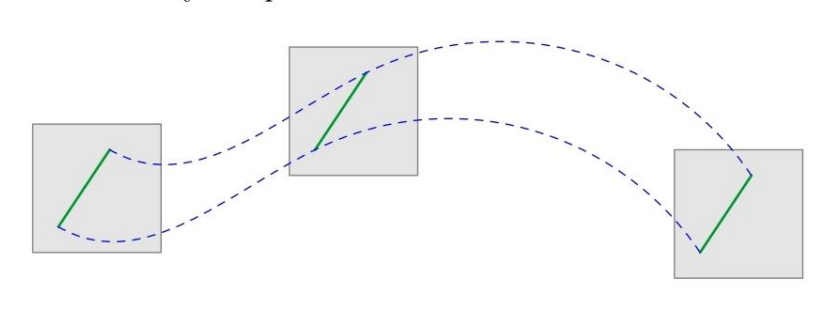
5.4. Преобразования Галилея

Преобразования Галилея - это математические соотношения, позволяющие описать связь между координатами и временем в различных инерциальных системах отсчёта.

Вот картинка, которая поможет понять преобразования Галилея.

5.5. Закон сложения скоростей

Закон сложения скоростей - скорость тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной системы.

5.6. Инвариантные и относительные величины

5.7. Преобразования ускорений

Это процесс перехода от одной неинерциальной системы отсчёта к другой.

5.8. Следствия преобразований Галилея

Обратим внимание, что единственное утверждение, которое мы описали преобразованиями Галилея - это взаимосвязь координат в разных инерциальных системах отсчёта.

А все остальные величины, например, скорость, ускорение - это следствия преобразований Галилея.

Так же из преобразований Галилея вытекает равенство расстояний между точками во всех инерциальных системах отсчёта.

6.1. Равномерное движение материальной точки по окружности.

Равномерное движение материальной точки по окружности - это движение при котором за равные промежутки времени тело проходит дуги равной длины, то есть модуль скорости постоянен.

6.2. Период и частота обращения.

Период обращения - это время, за которое тело совершает один оборот.

Частота обращения - это количество оборотов тела за единицу времени.

6.3. Описание движения с помощью линейных и угловых переменных

К линейным переменным относятся:

• Скорость v, ускорение a, радиус-вектор r, координаты x и y.

К угловым переменным относятся:

• Угловая скорость ω, угловое ускорение ε, угол φ.

6.3.1. Основные величины

Угловая скорость - это векторная величина, определяющая быстроту изменения угла между радиус-вектором и осью Ox.

Угловое ускорение - это векторная величина, определяющая быстроту изменения угловой скорости.

6.4. Закон движения

Закон движения здесь очень простой.

6.5. Центростремительное ускорения

Центростремительное ускорение - это ускорение, направленное в центр окружности, по которой движется тело.

Вывод

6.6. Направление центростремительного ускорения

Вектор центростремительного ускорения направлен в центр окружности, по которой движется тело.

Центр всегда находится под углом 90° к скорости, поэтому центростремительное ускорение называют также нормальным ускорением.

Вывод

Для того чтобы в этом разобраться снова воспользуемся рисунком.

7.1. Скорость и ускорение при криволинейном движении

Сопровождающая система координат.

Это делается с целью упростить задачу, так как мы можем представить криволинейное движение в виде нескольких дуг окружностей, по которым движется тело.

Мгновенная скорость всегда направлена по касательной к траектории.

7.2. Тангенциальное и нормальное ускорение

Тангенциальное ускорение - это ускорение, характеризующее быстроту изменения модуля скорости.

Нормальное ускорение - это ускорение, характеризующее быстроту изменения направления скорости.

7.3. Равнопеременное движение по окружности

Равнопеременное движение по окружности - это движение, при котором угловое ускорение постоянно.

7.4. Угловое ускорение

Угловое ускорение - это векторная величина, определяющая быстроту изменения угловой скорости.

7.5. Связь тангенциального и углового ускорения

Тут просто диффенцируя обе части равенства мы получаем связь между тангенциальным и угловым ускорением.

8.1. Движение тела, брошенного под углом к горизонту

Это движение тела, которое брошено под углом к горизонту. (литералли)

8.2. Законы движения

8.3. Максимальная дальность, высота полёта и время полёта

Между этими величинами есть следующие связи:

8.4. Уравнение траектории

Получаем уравнение траектории, подставив t из первого уравнения во второе.

8.5. Разложение вектора ускорения свободного падения на тангенциальную и нормальную составляющие

Просто нарисуйте рисунок и всё станет понятно.

9.1. Первый закон Ньютона

Первый закон Ньютона: "Существуют такие системы отсчёта, относительно которых свободное тело движется равномерно и прямолинейно".

Свойство свободного тела сохранять свою скорость называется инерцией.

9.2. Способ выбора инерциальной системы отсчёта

При выборе инерциальной системы отсчёта нужно учитывать, что она не должна быть подвержена внешним нескомпенсированным силам со стороны других тел.

Часто в качестве инерциальной системы отсчёта выбирают земную поверхность.

9.3. Сила как мера взаимодействия двух тел

Сила - это векторная физическая величина, которая характеризует взаимодействие одного тела на другое.

Ускорение тела пропорционально силе, действующей на тело. Отсюда следует, что если тело движется равномерно и прямолинейно, то на него не действуют силы.

9.4. Измерение сил

Динамометр - это прибор, который позволяет измерить силу, действующую на него.

Обычно динамометр представляет собой пружину, которая растягивается под действием силы. Он основан на законе Гука.

Вот такой прибор называется динамометром.

9.5. Векторный характер силы

Так как ускорение тела пропорционально силе, действующей на тело, а ускорение - это векторная величина, то сила также является векторной величиной.

Это опять же ссылает нас на второй закон Ньютона.

9.6. Сложение сил, действующих на материальную точку

Если на материальную точку действуют несколько сил, то считается что на неё действует их векторная сумма - называемая равнодействующей / результирующей силой.

9.7. Единицы измерения силы

Ньютон - это единица измерения силы в СИ. Это произведение массы на ускорение.

9.8. Масса

Масса - это фундаментальная физическая величина, характеризующая сразу несколько свойств тела:

9.9. Измерение массы

Существуют неограниченное количество способов измерения массы.

Но вот некоторые из них:

9.10. Единицы измерения массы

Килограмм - это единица измерения массы в СИ.