Физика 3
Билет 20.
20.1. Консервативные силы
Консервативные силы - это силы, работа которых не зависит от от траектории движения тела, а определяется от начального и конечного положения тела.
Как следствие, работа консервативных сил равна нулю для замкнутых траекторий.

20.2. Диссипативные силы
Диссипативные силы - это силы, работа которых зависит от траектории движения тела.
Иначе говоря, это любая силы, которая не является консервативной.
Как следствие, работа диссипативных сил не равна нулю для замкнутых траекторий.

20.3. Работа силы тяжести и силы упругости
Заметим, что обе силы консервативные. Это можно понять, если провести мысленный эксперименты с маятниками из нити и пружины. Обе системы в идеальных условиях будут работать бесконечно долго, а это значит что работа замкнутой траектории равна нулю.

Очевидно, что работа сил тяжести и силы упругости отрицательна:
20.4. Работа сил трения
Про работу сил трения можно лишь сказать, что она всегда отрицательна.
Вывод

20.5. Потенциальная энергия системы взаимодействующих тел
Можно сделать вывод, что в идеальных условиях механическая энергия системы взаимодействующих тел сохраняется.
20.6. Потенциальная энергия деформированной пружины
Сила упругости является консервативной, поэтому её величина зависит от величин x_1 и x_2.

20.7. Потенциальная энергия тела в гравитационном поле Земли
Рассмотрим работу силы тяжести в гравитационном поле Земли.
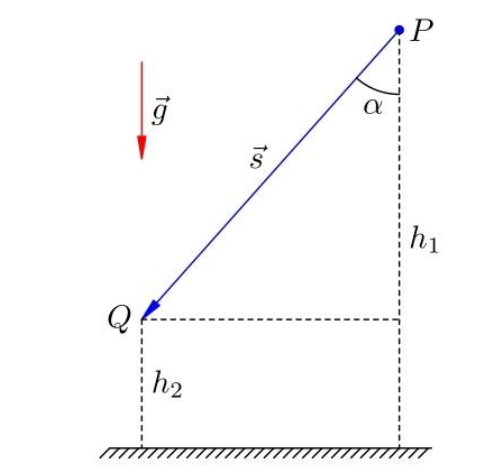
Энергию связанную с силой тяжести называют потенциальной энергией в поле тяготения.
20.8. Вторая космическая скорость
Вторая космическая скорость - это минимальная скорость, которую должен иметь космический корабль, чтобы покинуть гравитационное поле Земли.
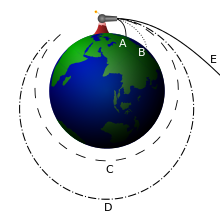
Основная идея следующая: Пусть тело падает с высоты R до центра Земли. Мы можем вычислить минимальную работу, которую нужно совершить, чтобы вытащить тело из гравитационного поля Земли.

Билет 21.
21.1. Закон изменения механической энергии системы тел
Отсюда следует, что в замкнутой системе изменение механической энергии равна работе внутренних сил трения.
21.2. Закон сохранения механической энергии
Закон сохранения механической энергии - это закон, согласно которому в идеальных условиях механическая энергия замкнутой системы тел сохраняется.
21.3. Упругий и неупругий удар
Абсолютно упругий удар - это удар, при котором относительная скорость первого тела до и после удара по модулю не меняется.

Абсолютно неупругий удар - это удар, при котором относительная скорость первого тела после удара равна нулю.

Билет 22.
22.1. Момент силы относительно оси вращения
Плечо силы - это минимальное расстояние от оси вращения до прямой, по которой приложена сила. (перпендикулярно)

Как видно, плечо перпендикулярно прямой, по которой приложена сила.
Момент силы - это произведение силы на плечо силы.

Как следствие, момент силы относительно оси вращения равен нулю, если сила приложена к оси вращения.
К таковым относят например (не во всех случаях) силу тяжести и силу трения.
22.2. Сложение сил, действующих на твёрдое тело, с учётом линий их действия
В целом, при решении задач, бывает полезным заменить несколько сил одной равнодействующей силой.
Это есть сложение сил, действующих на твёрдое тело, с учётом линий их действия.
Частный случай: сложение пересекающихся сил.
Если есть несколько сил, действующих на твёрдое тело, и их линии действия пересекаются в одной точке, то сумма моментов этих сил равна моменту равнодействующей силы.
22.3. Понятие равнодействующей силы
Равнодействующая сила - в контексте статики это сила, которая приложена к твёрдому телу, момент которой равен сумме моментов всех сил, действующих на тело.
22.4. Сложение параллельных сил
Ещё один частный случай - это сложение параллельных сил.

22.5. Пара сил
Пара сил - это две равные по модулю, противоположно направленные параллельные силы, приложенные к разным точкам твёрдого тела.

Момент пары сил равен моменту одной из сил пары относительно точки приложения другой силы.
Как следствие, пара сил не создаёт поступательного движения тела, а только вращательное.
22.6. Центр тяжести
Центр тяжести - это точка, в которой можно считать сосредоточенной вся масса тела.
Отсюда вытекает, что центр тяжести тела совпадает с центром масс тела (не всегда).

Как следствие, ось, расположенная в центре масс (центре тяжести) тела, имеет нулевой момент силы тяжести.
Билет 23.
23.1. Момент импульса частицы относительно оси вращения
Момент импульса - это произведение импульса на плечо импульса.
Тут аналогия с моментом силы, просто за силу берём импульс.
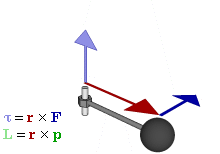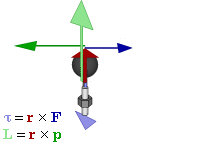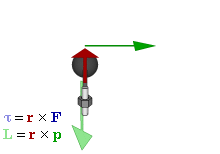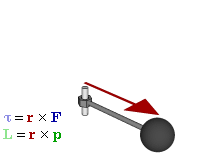
Как следствие, момент импульса относительно оси вращения равен нулю, если импульс приложен к оси вращения.
23.2. Момент импульса твёрдого тела
Моментом импульса твёрдого тела называют сумму моментов импульсов всех частиц тела.
23.3. Закон сохранения момента импульса
Закон сохранения момента импульса - это закон, согласно которому если момент сил внешних сил равен нулю, то момент импульса замкнутой системы тел сохраняется.
Билет 24.
24.1. Плоскопараллельное движение твёрдого тела
Плоскопараллельное движение твёрдого тела - это движение тела, все точки которого движутся по параллельным плоскостям.
24.1.1. Утверждение 1
Любое плоскопараллельное движение твёрдого тела можно представить как наложение двух движений: поступательного и вращательного.
Доказательство

24.2. Проскальзывание
Когда мы говорим об отсутствии проскальзывания, мы имеем в виду, что сила трения покоя не переходит в силу трения скольжения.
В случае наличия качения с проскальзыванием вперёд, то скорость вращения по величине меньше скорости движения оси диска.
Если же качение с проскальзыванием назад, то скорость вращения по величине больше скорости движения оси диска.
24.3. Мгновенный центр вращения
Мгновенный центр вращения - это точка, вокруг которой в данный момент вращается тело.
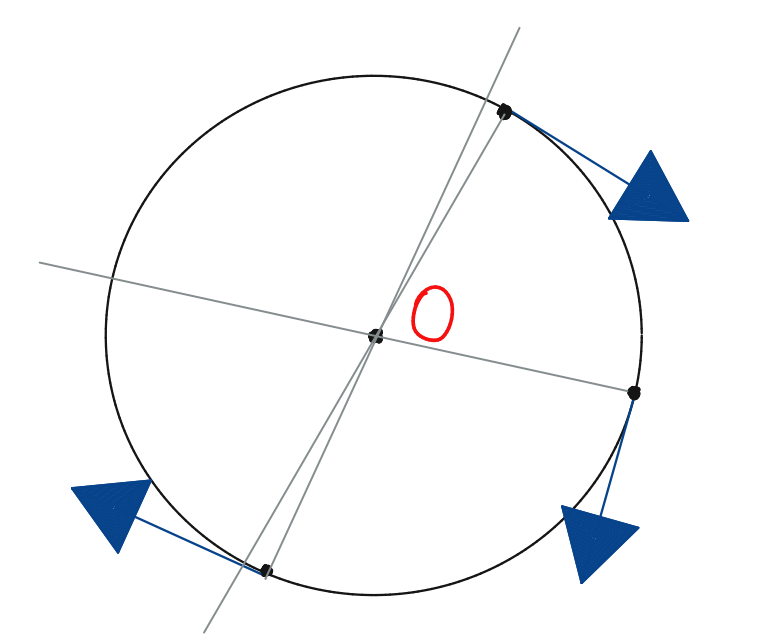
В данном случае, точка O является постоянным центром вращения.
А точка соприкосновения с землёй является мгновенным центром вращения.
Можно выделить следующие свойства МЦВ:
Его скорость в данный момент равна нулю.
Относительно него вращается в данный момент тело.
Билет 25.
25.1. Уравнение вращательного движения твёрдого тела
Оно имеет такой же вид, как и в случае вращения относительно неподвижной оси для центра масс тела.
Объяснить это крайне просто. Представим
25.2. Момент инерции
Момент инерции - это величина, которая характеризует инертность тела для вращения относительно оси вращения.
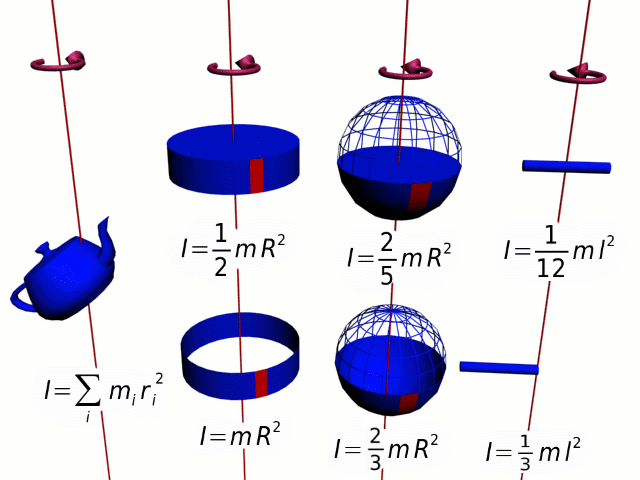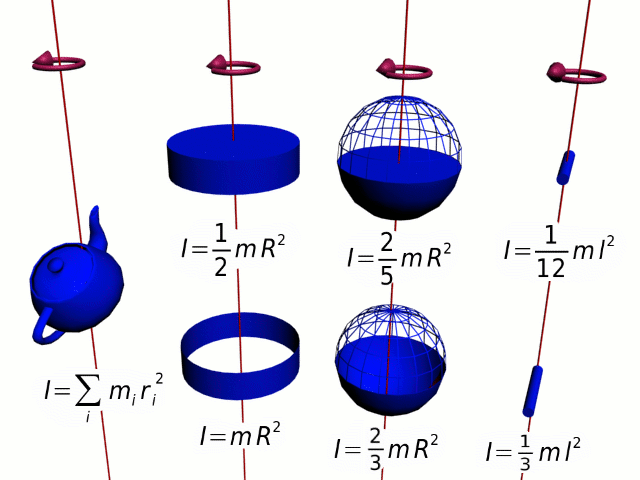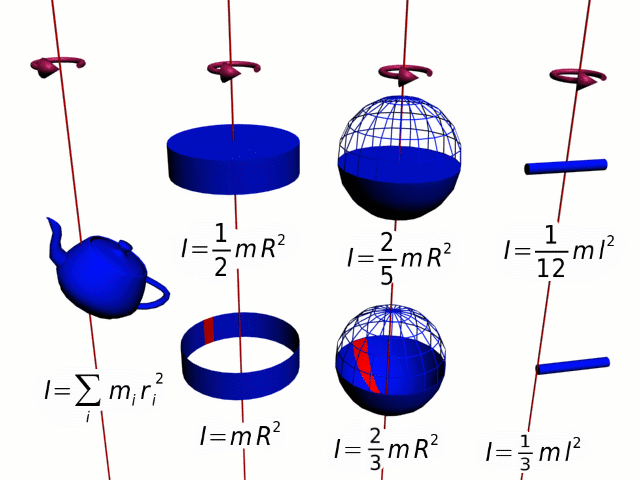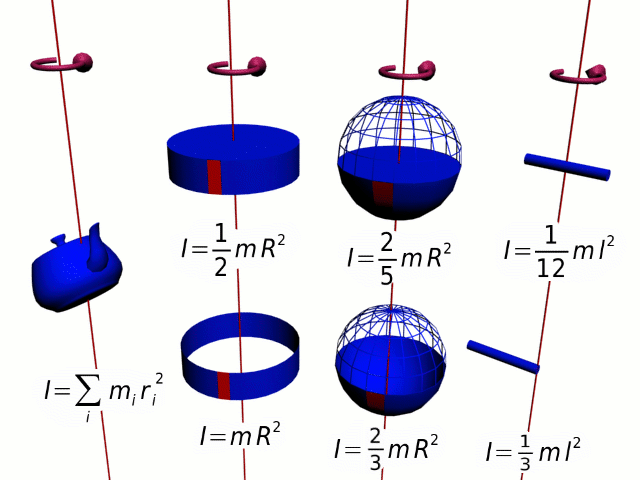
25.3. Теорема Гюйгенса-Штейнера
Теорема Гюйгенса-Штейнера - это теорема, которая позволяет вычислять момент инерции тела относительно произвольной оси, зная момент инерции в другой оси, параллельной первой.
Точная формулировка
Момент инерции тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между этими осями.

Билет 26.
26.1. Теорема Кёнига
Кинетическая энергия системы частиц равна сумме кинетической энергии поступательного движения (центра масс) и кинетической энергии вращательного движения (относительно центра масс).
Доказательство

Основная суть - расписать полную кинетическую энергию через относительную скорость.
26.2. Кинетическая энергия твёрдого тела
Билет 27.
27.1. Виды равновесия
Устойчивое равновесие - это равновесие, при котором при малом отклонении тела от положения равновесия, возникают силы, направленные так, чтобы вернуть тело в положение равновесия.

Неустойчивое равновесие - это равновесие, при котором при малом отклонении тела от положения равновесия, возникают силы, направленные так, чтобы отклонить тело ещё сильнее.

Безразличное равновесие - это равновесие, при котором при малом отклонении тела от положения равновесия, возникают силы, направленные так, чтобы оставить тело в новом положении.

27.2. Динамические условия равновесия частицы и твёрдого тела
Равновесие частицы наступает, когда на частицу действуют только консервативные силы, при этом потенциальная энергия частицы в стабильном состоянии имеет локальный минимум.
Равновесие частицы наступает, когда на тело действуют только консервативные силы, при этом потенциальная энергия тела в стабильном состоянии имеет локальный минимум.
27.2.1. Утверждение 1
Если на тело не действуют внешние силы (или они компенсируются), то сумма моментов сил вычисленных относительно любых двух параллельных осей равна нулю.
Доказательство
