Анализ 3

13.1. Виды окрестностей

Эпсилон-окрестностью точки a называется интервал (a - ε, a + ε) на оси y, где ε - положительное число.

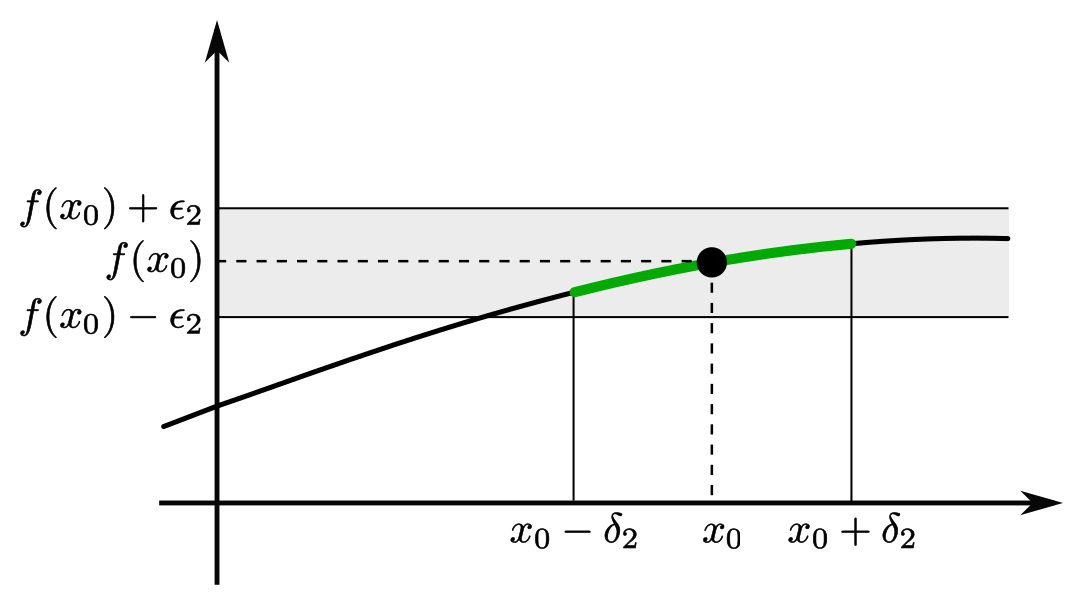
Дельта-окрестностью точки a называется интервал (a - δ, a + δ) на оси x, где δ - положительное число.

13.2. Ограниченность в окрестности

Функция f(x) ограничена в окрестности точки a, если существует такое число M, что для любого x из этой окрестности выполняется неравенство |f(x)| <= M.

13.3. Определение предела функции

Функция f(x) имеет предел A в точке a, если для любого числа ε > 0 существует такое число δ > 0, что для любого x из окрестности точки a выполняется неравенство |f(x) - A| < ε.

Это если что уже знакомство по Коши.

13.4. Свойства пределов функций