Анализ 1
Это актуальные билеты по сессии в СУНЦ МГУ. Надеюсь, что они помогут вам сдать экзамен.
1. Множества
1.1. Определение множества
Это совокупность различных объектов, называемых элементами множества.
При этом вся совокупность воспринимается как единое целое.

Это множество, элементами которого являются числа.

1.2. Типы множеств
Общая диаграмма типов множеств:
В конечном множестве количество элементов конечно. В таком множестве однозначно можно найти последний и первый элементы.
Например, множество натуральных чисел от 1 до 10.
В бесконечном множестве количество элементов бесконечно. В таком множестве нельзя найти или последний, или первый элементы.
Например, множество натуральных чисел, так как их бесконечно много.
В счётном множестве можно последовательно перечислять элементы (первый, второй, третий, ...).
Точная формулировка (для ботанов)
Счётное множество - множество, в котором можно установить взаимнооднозначное соответствие (биекция) между элементами этого множества и множества натуральных чисел. (При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством.)
В несчётном множестве нельзя последовательно перечислять элементы (первый, второй, третий, ...).
Точная формулировка (для ботанов)
Несчётное множество - множество, которое нельзя упорядочить в виде последовательности, в которой каждый элемент имеет свой номер.
1.3. Стандартные множества
Здесь представлены лишь самые базовые множества, которые вам понадобятся на экзамене.
Принято обозначать стандартные множества следующим образом:
1.4.0. Универсальное множество
Универсальное множество — это множество, содержащее все объекты и все множества.
Обычно универсальное множество обозначается буквой U и нужен лишь для того, чтобы убрать из любого множества ненужные элементы.
1.4.1. Операции над множествами





1.5. Подмножество
Одно множество может содержать все элементы другого множества. Такое множество называется подмножеством.

В данном случае A является подмножеством B:
1.6. Декартово произведение
Декартово произведение — это множество всех упорядоченных пар элементов двух множеств.
1.7. Мощность множества
Мощность множества — это количество элементов в множестве.
Не всегда мощность множества конечна, например, мощность множества натуральных чисел выражается дичью.
Два множества называются равномощными, если между ними существует взаимнооднозначное соответствие (биекция).
Множество B
Множество A
Иными словами, можно выразить следующее:
Функция f(x) не обязательно должна быть задана математической формулой, например множество простых чисел и множество нечётных чисел равномощны, но хоть f(x) в таком случае сложно задать, достаточно доказать что она существует.
Бесконечные множества:
Для обозначения мощности бесконечных множеств используют символ aleph, причём чем больше мощность множества, тем больше индекс у символа.
Мощности бесконечных множеств - целый отдельный раздел в теории множеств, но могу сказать в общих словах:
Для мощностей, как и в случае конечных множеств, имеются понятия: равенство, больше, меньше. То есть для любых множеств A и B возможно только одно из трёх:
|A| = |B|, то они равномощны.|A| < |B|, то B мощнее A -> в этом случае B содержит подмножество, равномощное A, но A и B не равномощны.|A| > |B|, то A мощнее B -> в этом случае A содержит подмножество, равномощное B, но A и B не равномощны.Ситуации, в которой A и B не равномощны и при этом ни в одном из них нет части, равномощной другому, невозможна по теореме Цермело.
Ситуации, в которой
|A| > |B|и|B| > |A|невозможна по теореме Кантора-Бернштейна.
И очень частным случаем является мощность множества действительных чисел:
В этом случае c - мощность континуума.
1.8.0. Термины свойств
Свойство — это утверждение, которое либо верно, либо неверно для каждого элемента множества.
Формула включения исключения в обычной формулировке несёт смысл, только если мы оперируем с конечным множеством чисел.
Однако на практических задачах (например по физике) часто даются конкретные величины, которые невозможно перечислить как множество.
В таком случае мы абстрагируемся от множеств и переходим на свойства, где:
Как могли заметить, принято:
свойства - строчными буквами, вычисления в основном с величинами
множества - заглавными буквами, вычисления в основном с элементами
Подробнее про булеву алгебру со свойствами можно почитать в этой статье.
1.8.1 Основная формула включений и исключений
Запомните формулу включений и исключений, она пригодится вам на экзамене. Формулировка в терминах множеств:
Есть ещё формулировка в терминах свойств:
Вот примеры задач которые можно решить с помощью этой формулы:
Найти количество чисел от 1 до 1000, которые делятся на 2, 3 или 5.
Найти количество чисел от 1 до 1000, которые не делятся на ни на 2, ни на 3, ни на 5.
Доказательство (для слабых)
Частный случай с кругами Эйлера

В данном случае мы можем воспользоваться кругами Эйлера, чтобы наглядно понять и выразить формулу включений и исключений.
Доказательство (для сильных)
Общий случай
2. Числовые функции
Числовой функцией с областью определения X и областью значений Y называется зависимость, при которой каждому элементу x из X по правилу f ставится в соответствие единственное значение y из Y.
2.1. Определение функции
Это отображение, которое каждому элементу из области определения ставит в соответствие единственный элемент из области значений.

Это множество, элементы которого являются аргументами функции.

Это множество, элементы которого являются значениями функции.

2.2. Когда функции равны?


2.3. Виды функций
Чётная функция — это функция, которая симметрична относительно оси ординат.

Нечётная функция — это функция, которая не является чётной.

Возрастающая функция — это функция, которая строго возрастает на всей области определения.

Убывающая функция — аналогично возрастающей, но строго убывает на всей области определения.

Неубывающая функция — это функция, которая не убывает на всей области определения.

Невозрастающая функция — аналогично неубывающей, но не возрастает на всей области определения.

2.4. Монотонность функции
Функция называется монотонно возрастающей/убывающей, если она строго возрастает/убывает/не изменяется на всей области определения.


С помощью монотонности мы можем сказать Пицыну: "Очева".
Например, в показательных уравнениях, если обе части уравнения монотонны и одна строго возрастает, а другая строго убывает, то уравнение имеет единственное решение.
3. Графики функций
3.1. Определение графика функции
График функции — это множество точек плоскости, координаты которых удовлетворяют уравнению функции.

Каждая из точек удовлетворяют следующему условию:
3.2. Цепочка преобразований графика функции
Ниже указан порядок преобразований графика функции:
Сжимаем/растягиваем график по оси абсцисс.
Сдвигаем график влево/вправо на.
Сжимаем/растягиваем график по оси ординат.
Сдвигаем график вверх/вниз.
Конечный результат:
3.3. Запоминаем абсциссу/ординату на графике
Вот так можно запомнить, какая из осей называется абсциссой, а какая — ординатой.

4. Обратная функция
4.1. Определение обратной функции
Обратная функция — это такая функция, которая отображает значения функции в аргументы. Чтобы можно было получить обратную функцию, функция должна быть взаимно-однозначной.

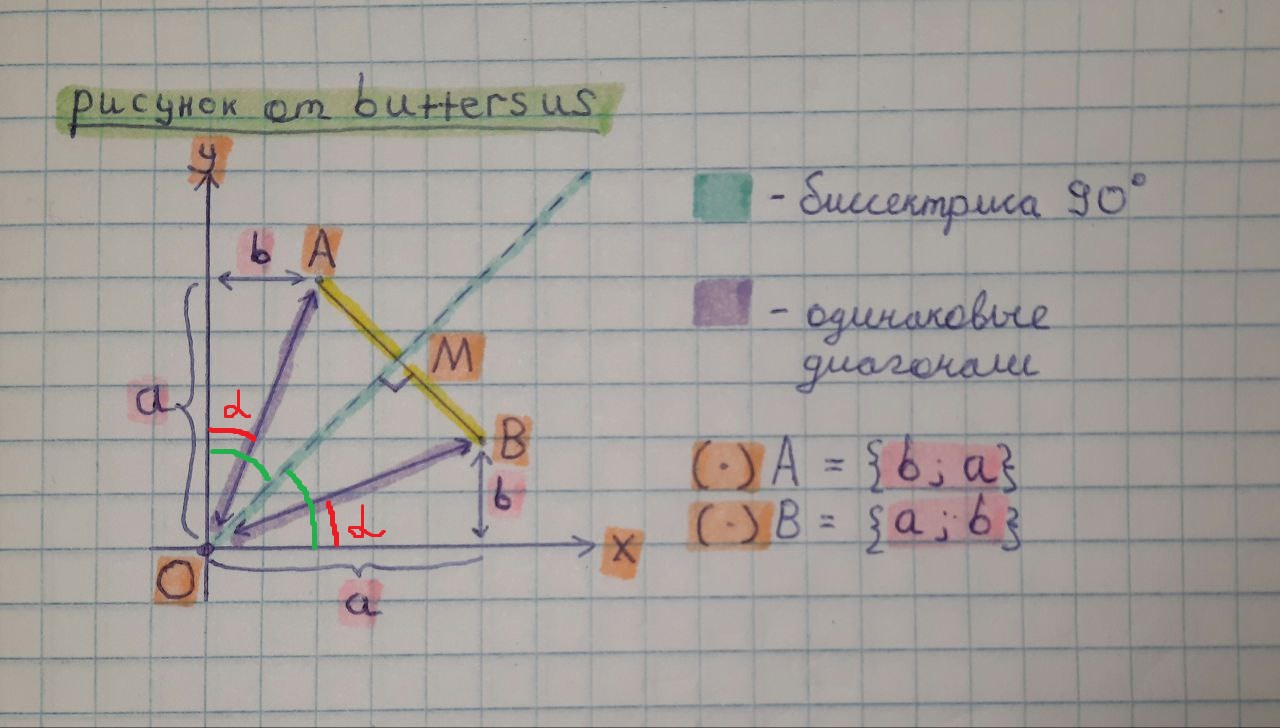
4.2. Симметрия графика обратной функции
Заметим, что график обратной функции симметричен относительно прямой y=x.

Доказательство
5. Продолжение...
Читайте дальше в следующей части.