Lexical Analysis
In this topic, we will discover the theory behind lexical analysis, and the most common algorithms used to implement it.
In my opinion, you can skip this topic if you are only interested in the practical side of compilers. However, it's still a good idea to read it, as in universities, it's usually taught before the practical side.
Overview
We will discover the next topics in this order:
Implementation
Implementation Details
Practical Problems
Foundations
Lexical analysis is the first phase of a front-end.
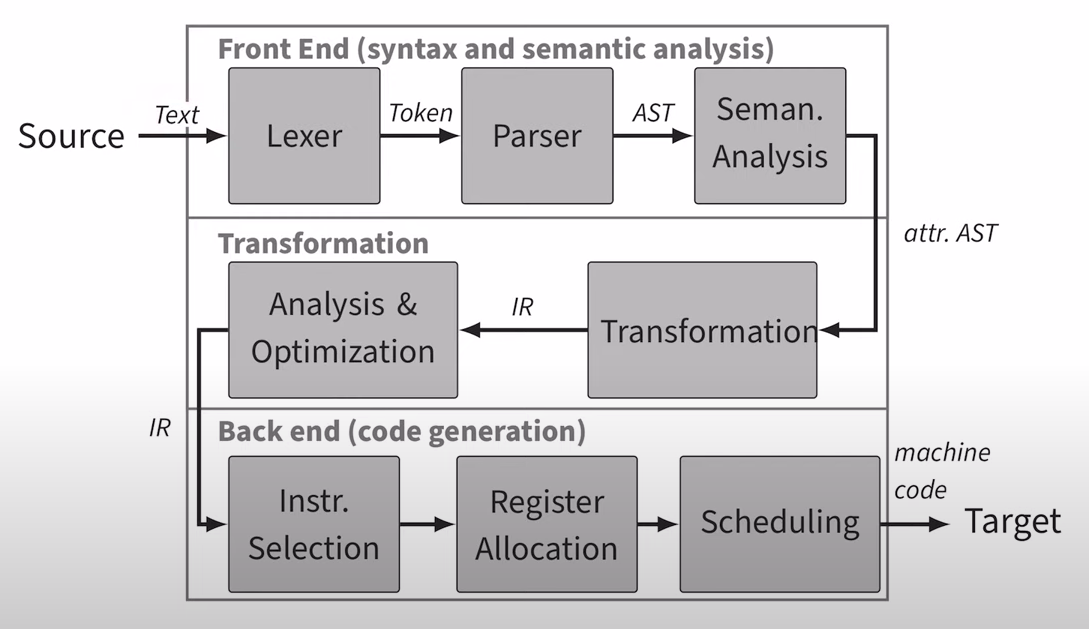
It takes the program as a sequence of characters, and produces a sequence of symbols called tokens.
Goals of lexical analysis:
Functionality: Produce tokens from the input program. It should be able to handle all valid programs.
Programmer Support: Provide useful error messages, correct common mistakes, and provide useful information to the programmer.
Remove Redundancy: Remove redundant information from the input program, such as comments and whitespace.
Identify Keywords: Identify keywords in the input program and separate them from identifiers. It's important as parser uses token types to determine the structure of the program.
Construct Symbol Table: Construct a symbol table for the input program. It's typically a map with all strings in the program, and instead of storing the string itself, it stores a key to the string in the symbol table. (Strings appear multiple times)
Notations
Before we start, it's nice to have a common understanding of regular expressions and their practical use.
Math behind Lexical Analysis
We are going to use a lot of mathematical notations in this topic, most of them are related to set theory.
Alphabets
The first thing we need to define is the alphabet of the language.
You can think of an alphabet as a set of characters. Characters are the smallest unit of a language, and they are used to construct words. The alphabet of a language is finite.
Now let's take a look at operations on alphabets.
They are pretty straightforward, these operations can remind you of regular expressions. Basically, now we are dealing with sets of strings.
Also, we can use default operations on sets, such as union, intersection, etc.
Examples
Words and Letters
In the previous section, we defined alphabets using characters and strings.
I prefer to use greek letters for words, and latin letters for characters.
But it's more correct to call them letters and words.
More formally, word is a concatenation of letters.
It's convenient to use the second notation, as it's more compact.
Concatenation of words is also a word.
Besides concatenation, there are also few other operations on words.
These are not words anymore, it's languages.
Examples
Languages
We call a set of words a language. L is a common notation for languages.
What is funny, it's already enough to define simple constructions, such as numbers.
Operations on languages produce new languages.
Examples
Regular Languages
Regular languages are languages that can be described using regular expressions.
More formally, regular languages more likely can find practical use, as they are easier to implement using finite state machines.
Regular Expressions
Each regular language can be described using regular expressions.
Expression | Language | Example words |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
We guess that you are already familiar with regular expressions, so we won't go into details.
To show that a language is regular, we can use next notation:
Automata
Finite state machines also known as automata are often used to describe regular languages. However, usage of automata is not limited to regular languages.
In the case of lexers, we are going to think of automata as program that implements regular expressions. This is the main part of the lexer.
Facts about automata:
It makes transitions from one configuration to another. (They are called states)
Each configuration consists of (the rest of) the input and some memory. (We use this information to determine the next state)
The type of memory determines its ability to recognize a class of languages.
A Non-Deterministic Finite-State Machine (NFSM)
One of the simplest automata is a non-deterministic finite-state machine.
Other parts will be clear after we see an example.
Example of NFSM
We use directed graph to represent NFSM.
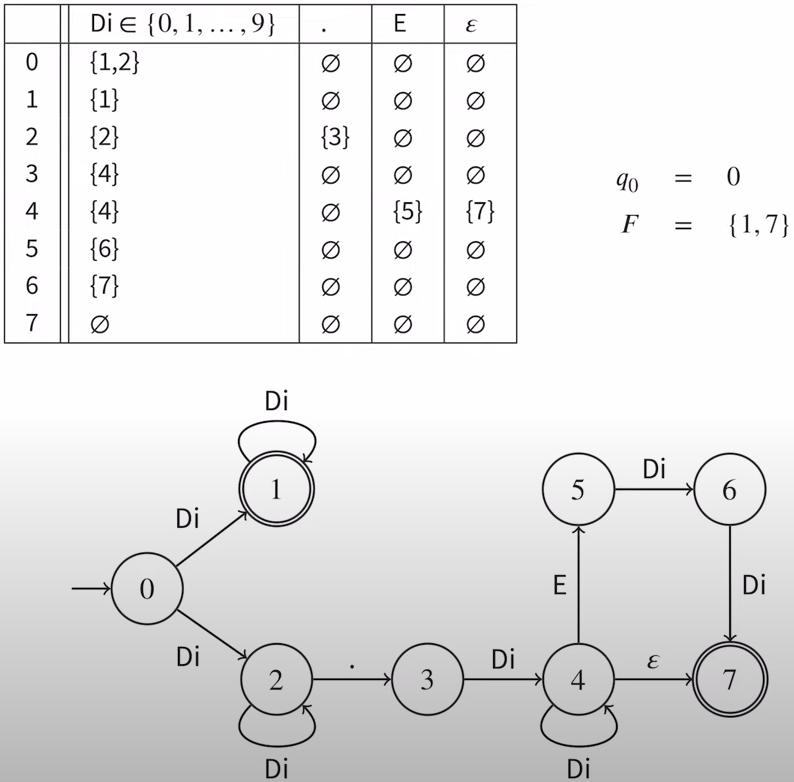
Let's take a look at fragments of NFSM:
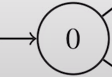- initial state (first state when we start the program)
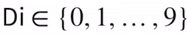- alphabet
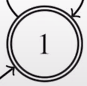and 
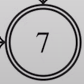- final states (with double stroke)
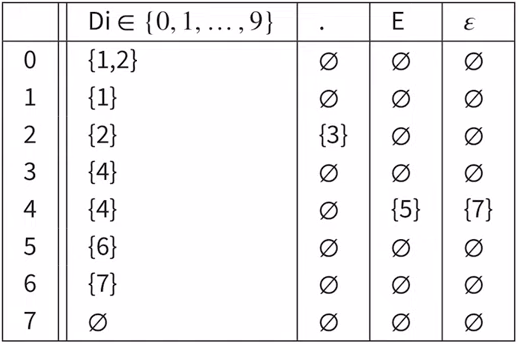- transition relation (table)
and 
- transition requirements as part of the transition relationstates are represented as circles
In this example, we have NFSM that recognizes fractional numbers with scientific notation. 2.14e3 as example.
The only problem with NFSM is that its time complexity is exponential, as we need to check all possible paths.
FSM to Lexical Analyzer
Of course, we can't use FSM (NFSM) as a lexical analyzer without any modifications.
Here's my diagram of how FSM is used in the lexical analyzer.
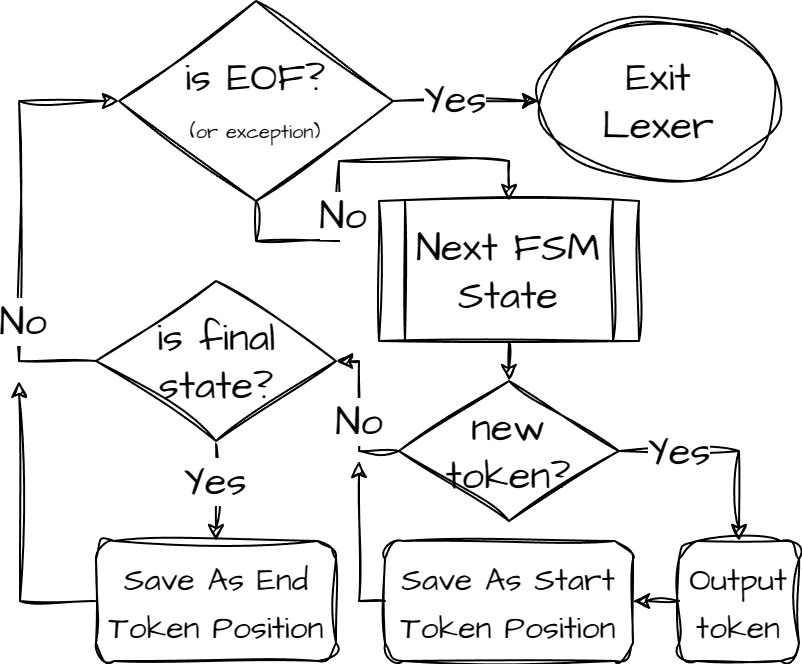
As you can see, each time we end new token, we need to reset the FSM to the initial state with the rest of the input.
Maximal Munch Strategy
Note, our FSM uses greedy strategy; it tries to match as many characters as possible.
It's shown in the diagram as saving the last end token position (if it's a final state).
Example
Let's assume we have the next input: 2.14e+s:
We save the last end token position a few times, the last one is
2.14.We can save 'e+' as part of the number if it ends with a digit like so:
2.14e+3.After it gets to the
s, we can't find any legal transition, so we end the token.It's important that in this case we are using non-deterministic automata, so we can try to find another token with
e+s.We will discover other approaches to handle this case later when we talk about deterministic automata.
The Language Accepted by the FSM
Firstly, let's define what configurations are.
Configuration is a pair of state and the rest of the input. It's used to desribe steps in formal way. Like so:
That operation is called transitive closure. To show more than one step, we can use reflexive transitive closure.
We can also define language using FSM.
Theorem 1
Finally, we can give a formal definition of regular languages.
Regular Language
Regular Expression
Constructive Proof 1
Firstly, we need to construct automata with one final state and one transition: 
Then we can decompose r and develop the NFSM according to the following rules: (until the whole expression is decomposed)
FSM | RegEx | Meaning |
|---|---|---|
| Union of two languages | |
| Concatenation of two languages | |
| Kleene star of a language (We are using epsilon transition to avoid collision with other transitions of `q` & `p`) |
Deterministic Finite-State Machine (DFSM)
In modern compilers, NFSM is not used anymore, since its time complexity won't allow us to implement big languages.
As you can guess, we are going to use deterministic finite-state machine:
Theorem 2
The good news is that DFSM can recognize the same languages as NFSM.
Constructive Proof 2
We can just think of each state as a set of states of NFSM. The DFSM simulates all possible transition paths under an input word in parallel.
Let's determine a set of new states:
Before we look at the formal algorithm, let's take a look at the example.
Example
Let's construct NFSM for the next regular expression: a(a|b)*.
|
|
|---|
It's convenient to use a table to represent the transition relation. By the way, diagram was generated by this online tool.
To construct set of states, we need to start from the initial state 0 and find all possible transitions, including epsilon transitions.
State | a | b |
|---|---|---|
0 | {1, 2, 3, 5, 8} | |
{1, 2, 3, 5, 8} | {2, 3, 4, 5, 7, 8} | {2, 3, 5, 6, 7, 8} |
{2, 3, 4, 5, 7, 8} | {2, 3, 4, 5, 7, 8} | {2, 3, 5, 6, 7, 8} |
{2, 3, 5, 6, 7, 8} | {2, 3, 4, 5, 7, 8} | {2, 3, 5, 6, 7, 8} |
We can apply one obvious optimization: remove duplicates.
State | a | b |
|---|---|---|
0 | {1, 2, 3, 5, 8} | |
{{1, 2, 3, 5, 8}, ...} | {2, 3, 4, 5, 7, 8} | {2, 3, 5, 6, 7, 8} |
Now we have only two states, and we can rename them to q_0 and q_1. Unoptimized and optimized versions are shown below.
Go play with this online tool to get more experience.
Formally, we can define the algorithm as follows:
DFSM Minimization
The last thing we need to do is to minimize DFSM. It means that we need to remove redundant states.